Harmonic Tide Analysis

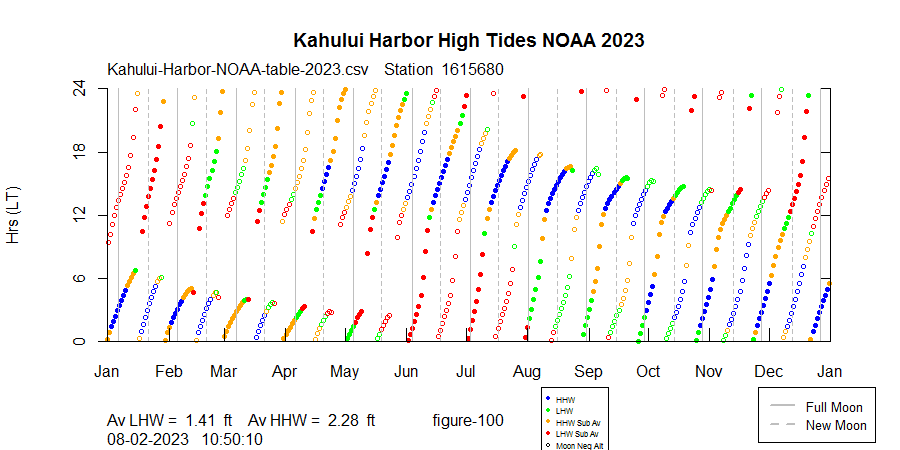
 We now have a good understanding, observationally, of what's going on with Maui's  high tide "holes". The holes appear when the tide shifts temporarily from semi-diurnal to diurnal. The morning high tide disappears and then reappears a few days later several hours later in the day, creating a hole in the time plot. 

 What is the underlying cause?  It seems clear that Maui's high tides are reacting in some way to the changing configuration of the Earth-Moon-Sun system.  Looking at the runs of high tides leading up to the "holes", one can almost feel the presence of a force that diverts and suppresses morning high tides in the first half of the year.  Is there a way to look under the hood? 

How Tides are Predicted

Most of you have probably seen diagrams of the forces produced by different Earth-Moon-Sun alignments, complete with tidal bulges and force vectors.  Great minds, beginning with Newton, have worked on mathematical descriptions of the forces that produce the tides.  Please see the reference blog if you are curious.  The forces are well understood for a perfect Earth with no continents, coastlines, and varying ocean depths.  In practice, it is not feasible to predict the tides from first principles as Newton attempted.  Instead, tide observations are made at many locations,  and the data are fitted to a sum of cosine functions, where each function is related to a known astronomical frequency.   Here are the top 4 cosines or harmonics (out of 25) for Maui:

Name Amplitude   Period (hrs)   Description

M2   0.6         12.422         Principal lunar semidiurnal 

K1   0.55        23.936         Lunar diurnal declinational

S2   0.31        12.000         Principal solar semidiurnal 

O1   0.31        25.825         Lunar diurnal declinational

You can think of the tide values being approximated by:

tide(t) = .6cos(wm2*t ) + .55cos(wk1*t ) + .31cos(ws2*t) + .31cos(wo1*t), 

where wm2, wk1, ws2, and wo1 are the speeds of each harmonic.  For you engineers the starting phase angle for each harmonic is not shown to keep it simple.

The Amplitude column represents the relative strength of each harmonic after the observed data have been fitted.  M2, a harmonic owing to the twice daily meridian crossing of the Moon, is the largest.  Its period, 12.422 hrs, is half the length of the mean lunar day, which is about 24 hrs 50 mins.  Since the lunar day is longer than the solar day by about 50 mins, you will frequently see that high tides will be 50 mins later each day.  50 minutes is only an approximation, and the actual daily delay can vary widely.

In the case of Maui you can see that the #2 harmonic is K1, a diurnal harmonic owing to the movement of the moon and the sun above and below the equator, ie "declinational".  S2 is the harmonic owing to the Sun's twice daily meridian crossing, and O1 is another declinational harmonic at a slightly different frequency.  Not shown are harmonics owing to the elliptical nature of the Moon's orbit.  While significant, they are smaller than the ones shown.

NOAA publishes all 25 "harmonic constituents" for Maui, and there are several tide prediction software packages that enable the user to predict tides based on the harmonics.  One in particular, "OCE" for the R environment, allows the user to select which harmonics participate in the prediction.  

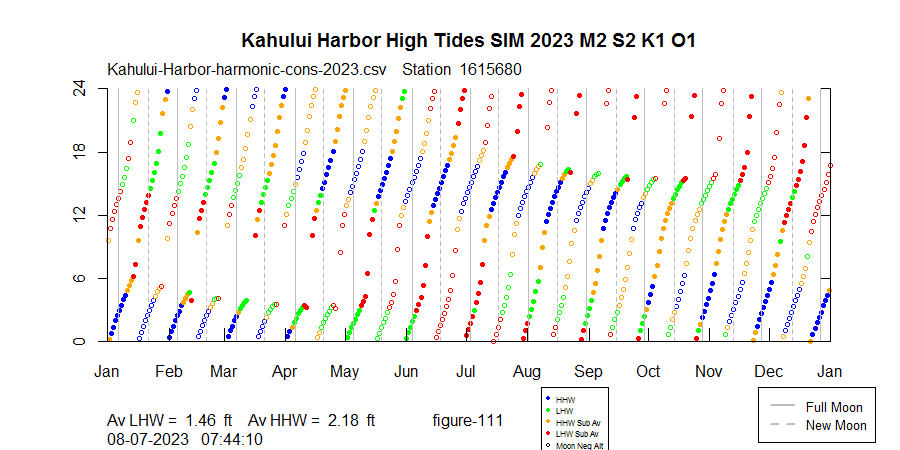
How well can only the top 4 harmonics approximate Maui's tide patterns?  The plot below uses only the top 4 harmonics, and it approximates the NOAA predictions pretty well:

Let's look at the actual cosine functions that pertain to the hole that develops on March 13, 2023.  The total tide is offset upwards for visibility:

S2 and K1 have very similar periods so, over the span of a few weeks, their phase relationship remains consistent.  On March 13, and in fact for much of the first half of the year, the S2/K1 combination contributes negatively to the total in the first half of the day.  What tips the scale is the O1 minimum moving through.  The combination of S2,K1, and O1 being negative overwhelms the normally dominant M2 harmonic, with the result that the morning high tide is suppressed out of existence.  As O1 continues to move through, in a few days it is no longer synched up with K1, and a morning high tide shows again on the 17th.  In the figure above the lines show that by March 17 the O1 minimum has moved away from the M2 maximum, allowing the M2 tide to re-assert itself.

Physical Significance of Individual Harmonics

Since K1 and O1 are representative of the Moon's monthly journey above and below the equator, it might be interesting to look at lunar declination relative to the yearly plot:

At first glance it looks like the minima in lunar declination line up nicely with the holes, but a closer look shows that the declination curve precesses evenly throughout the year and we can't make a ready correlation.  

Let's look back at the individual harmonics:

The S2 harmonic, owing to the Sun's twice daily meridian crossing, is fixed in place relative to the beginning of each day, as it should be since we keep time on a 24 hour clock and the S2 period is 12 hours.  It would have been satisfying to see the peaks of the S2 harmonic aligned with local noon and midnight, but that is not the case.  Instead we see the peaks at about 2am and 2pm.  We do see that Maui's tides typically show a 0 to 4 hour lag, so maybe this lagged S2 makes sense.  

Also shown are the times of upper and lower transit, and once again we see the M2 (blue)  harmonic is lagged by a few hours from the astronomical event which generates it, the twice daily passing of the Moon through the local meridian.  

It is not so easy to make a correlation between the K1 and O1 harmonics.  These have diurnal periods but are generated by the Moon's monthly trip above and below the celestial equator.

Conclusions:

We've taken a close look at Maui's yearly tide patterns and have looked under the hood at the astronomical influences.  

Do we find correlations that can explain the "holes" we see in Maui's winter high tides?  It's not that simple.

Let me quote from an email from Dan Kelley, professor of oceanography at Dalhousie University, Halifax, Canada:

I suspect surfers might want a "why" answer that is along the lines of "the sun is more nearly overhead at certain times of the year, owing to the tilt of the earth's rotation axis to the plane of the earth's orbit around the sun" but that is a bit made-up.  Which constituents are dominant in any given area depend on the shape of the ocean there, nearby, and far away.  Think of a bowl of soup sloshing as you walk across a food court, and now imagine that the bowl is not symmetric, but instead has deep and shallow portions that make for complicated sloshing.

In order to predict the tides from first principles as Newton attempted, one would have to take account of everything that is known about the Pacific ocean, including the shape of every coastline and the complete bottom contours, and then feed that data into a set of complicated non-linear hydrodynamic equations.  

It is true that at Maui, the K1 and O1 harmonics are more dominant relative to the M2 harmonic than at San Francisco or Fiji:

         M2   S2   K1   O1   (K1+O1)/M2

Maui     .6  .31  .55  .31    1.43

SFran  1.89  .45 1.21  .75    1.04

Fiji   1.85  .3   .31  .15     .25

The K1 and O1 are harmonics meant to account for the Moon's (and the Sun's) movement above and below the equator.

The ratio (K1+O1)/M2 is commonly used to classify locations as to the type of tide.  On the scale used by NOAA, Fiji would be classified as semi-diurnal, and both Maui and San Francisco would be "mixed, mainly semi-diurnal", although one might suspect that Maui has many more diurnal days than San Francisco.

If we only had the M2 harmonic owing to the Moon's twice daily meridian crossings, then we would have perfectly semi-diurnal tides.  But when a harbor has strong diurnal K1 and O1 harmonics, then those harmonics can occasionally overwhelm the one of the M2 harmonic high tides, creating a diurnal or once daily tide.

If one insists on some kind of correlation to the astronomical forcing functions, one could say that at Maui the "bowl of soup" shows a resonance at the K1 and O1 frequencies that combines to produce the tidal holes and overall weak winter high tides during the day.  But even this might be going too far for  our oceanographer friends, who told me "You are focusing on the inputs.  We prefer to look at the outputs."

Are the harmonic constituents physically real or not?  Here is a quote from Hicks, p43:

The Luni-solar Declinational diurnal constituent, K1, and the Principal Lunar Declinational diurnal constituent, O1, are also artificial constituents designed to simulate the cycle of maximum declination to maximum declination of the moon.

What does Hicks mean by "artificial"?  One gets the feeling that tide experts view the "bowl of soup" as a black box whose inner workings are unknown but can be approximated by these convenient quantities known as harmonics.  Yet, a spectrum taken from real world observations will show the lines M2, S2, K1, O1, etc.  (from Parker, figure 2.17):

Whatever you believe about the astronomical forces affecting Maui's tides, there is no denying that extra caution is required over Maui's shallow reefs during much of the day in winter.